You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
2 years ago | |
|---|---|---|
| src | 2 years ago | |
| .gitignore | 2 years ago | |
| Cargo.lock | 2 years ago | |
| Cargo.toml | 2 years ago | |
| README.md | 2 years ago | |
| screenshot.png | 2 years ago | |
README.md
Texture Packing
A simple rectangle packing implementation intended to be used for creating texture atlases.
Notes:
- No claim to be particularly fast or to pack particularly efficiently, the priority was simplicity
- Assumes that swapping rectangle dimensions is allowed (e.g. a 90 degree rotation or transposition)
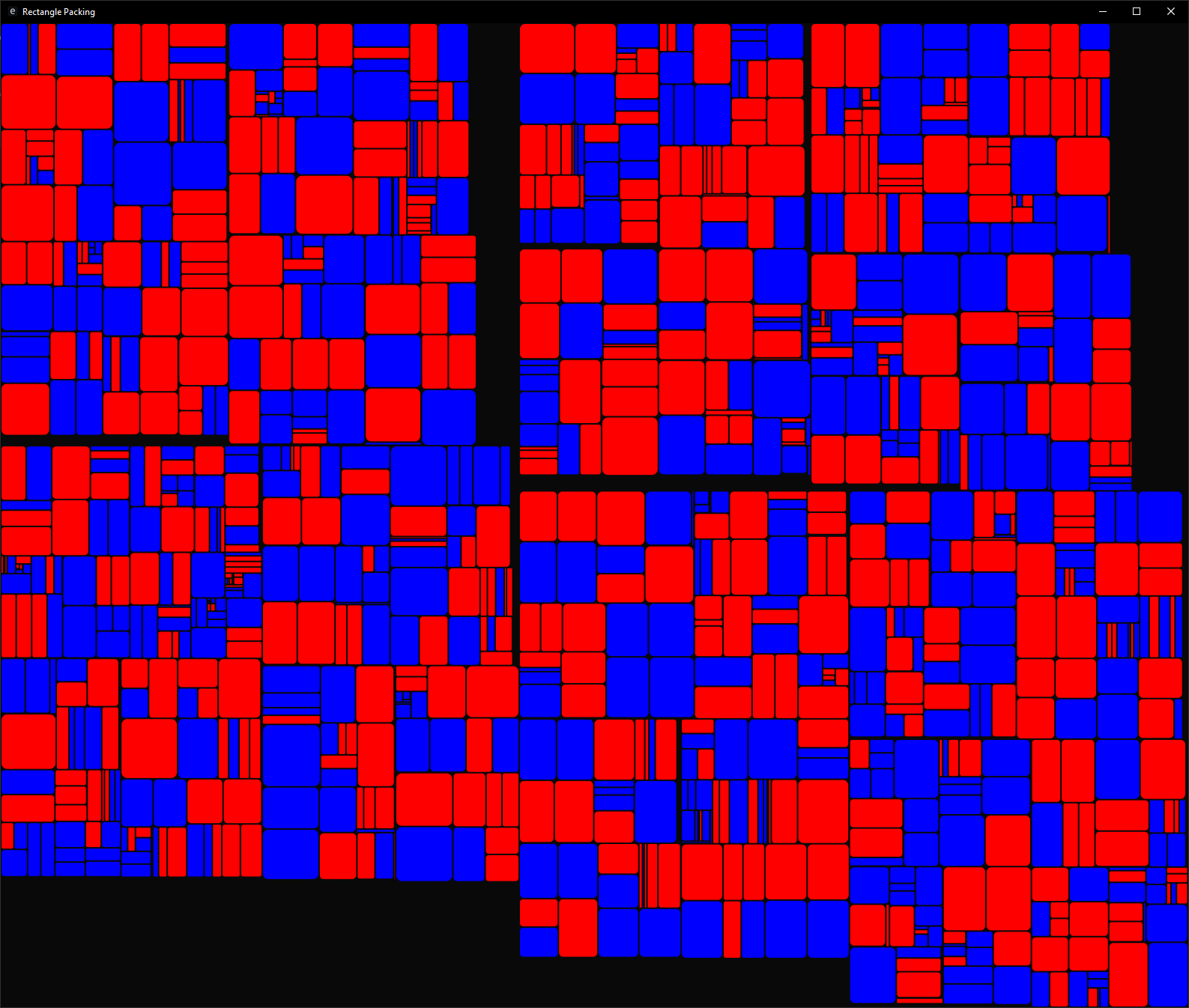
- Press
rto generate and pack a new set of rectangles - Blue rectangles are in their original orientation and red are transposed
Explanation
For another project I needed to pack a texture atlas and wanted a simple algorithm that did better than a naive implementation. This is the first algorithm that I could come up with, very roughly inspired by the basic algorithm to build Huffman code tables. Therefore, I'm not sure if this algorithm already has a name. Here is a very rough outline of the algorithm
- First, the list of rectangles is transposed so that the width of each rectangle is the larger of the two dimensions.
- Next, the list of rectangles is sorted by width (the larger of the two dimensions) followed by height in the case of equal widths.
- While there are more than 2 rectangles left in the list, do the following:
- The two smallest rectangles are removed from the back of the list and merged into a new rectangle.
- They are merged into a new rectangle where the width is the largest of the widths of the two merged rectangles and the height is the sum of the height of the two merged rectangles.
- References to each of the two merged rectangles are attached to the new rectangle.
- The new rectangle is transposed if the new height is larger than the new width.
- The new rectangle is inserted back into the list such that it is still sorted.
- Now, there is one rectangle and a binary tree structure describing how the rectangles are packed
- The binary tree structure is traversed depth first to compute the final positions and orientations, which are returned in a list.